Unique Tips About What Is The Value Of I3 If I1 2A And I2 3A

A Microscopic View Of Electric Circuits Ppt Download
Cracking the Circuit
1. Understanding the Basics
Ever felt like you're wading through a jungle of wires and currents? Don't worry, we've all been there! Let's tackle a common electrical puzzle: finding the value of current I3 when you already know I1 is 2 Amperes (2A) and I2 is 3 Amperes (3A). This isn't some arcane magic; it's all about a simple, yet powerful, principle called Kirchhoff's Current Law (KCL).
Imagine a water pipe splitting into multiple streams. The total amount of water flowing into the junction must equal the total amount of water flowing out of the junction. Kirchhoff's Current Law says the exact same thing, but for electrical current. It states that the algebraic sum of currents entering and leaving a node (a junction in a circuit) must be zero. Think of it as electrical conservation of energy.
Now, why is this important? Because it gives us a powerful tool to analyze circuits and figure out unknown currents, like our elusive I3. It's the electrical equivalent of knowing your budget and figuring out where your money is going (or in this case, where the electrons are flowing!).
So, KCL is the key. But how do we actually use it to find I3? Lets dive into that in the next section. Consider this the 'once upon a time' of our electrical story.
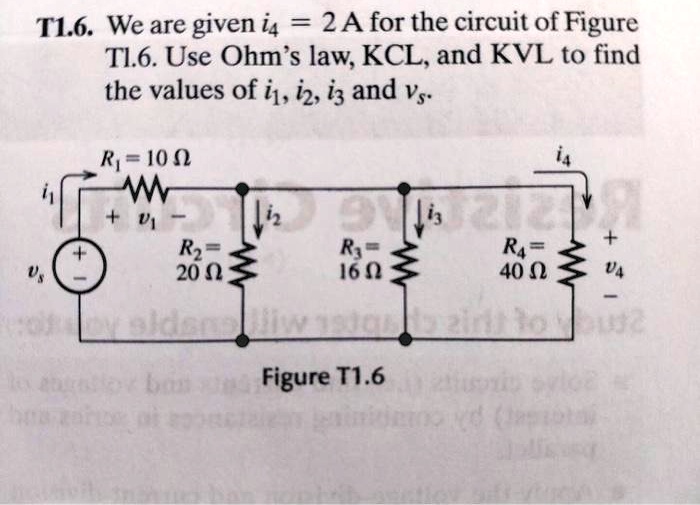
T16 We Are Given I4 2a For The Circuit Of Figure Tl6 Use Ohm S Law Kcl
Applying Kirchhoff's Law
2. Setting Up the Equation
Alright, time to put on our thinking caps and do a little electrical arithmetic! The specific arrangement of the currents I1, I2, and I3 at the junction is absolutely critical. We need to know which direction each current is flowing relative to the node (the junction point). Is it going in? Is it coming out?
Let's assume a simple scenario: Both I1 and I2 are flowing into the node, and I3 is flowing out of the node. In this case, Kirchhoff's Current Law tells us that: I1 + I2 = I3. The total current flowing into the junction (I1 + I2) must be equal to the total current flowing out (I3).
Now, let's plug in the values we know: I1 = 2A and I2 = 3A. So, the equation becomes: 2A + 3A = I3. Simple enough, right? It's like adding apples and oranges, except these are amps and... well, more amps.
Therefore, I3 = 5A. That's it! We've found the value of I3. But hold on, there's always a "but," isn't there? What if the currents are flowing in different directions?

Solved Use Mesh Analysis To Obtain I1,i2, And I3 In The
Different Directions, Different Signs
3. Accounting for Current Flow Direction
Here's where things can get a little trickier, but don't fret! The direction of the current matters. We need to assign a sign (positive or negative) to each current based on whether it's entering or leaving the node. By convention, we usually consider current flowing into the node as positive and current flowing out of the node as negative (or vice-versa, as long as you're consistent!).
Let's say, for example, I1 is flowing into the node (2A), but I2 is flowing out of the node (-3A), and I3 is still flowing out (-I3). Then, using KCL: I1 + I2 + I3 = 0. Plugging in the values: 2A + (-3A) + (-I3) = 0. Simplifying, we get: -1A - I3 = 0. Therefore, I3 = -1A. The negative sign here indicates that I3 is actually flowing into the node, not out of it as initially assumed. This change in direction can happen based on how circuit is setup and what you are trying to achieve.
See? It's all about paying attention to the direction of current flow. Think of it like playing tug-of-war. If both teams are pulling in the same direction, the rope moves that way. But if they're pulling in opposite directions, the rope moves towards the stronger team. The same principle applies to currents in a circuit.
The sign convention makes all the difference, and without it, we would be nowhere and just making mistakes on the calculation. So make sure you follow these steps to ensure that the calculation are all correct.
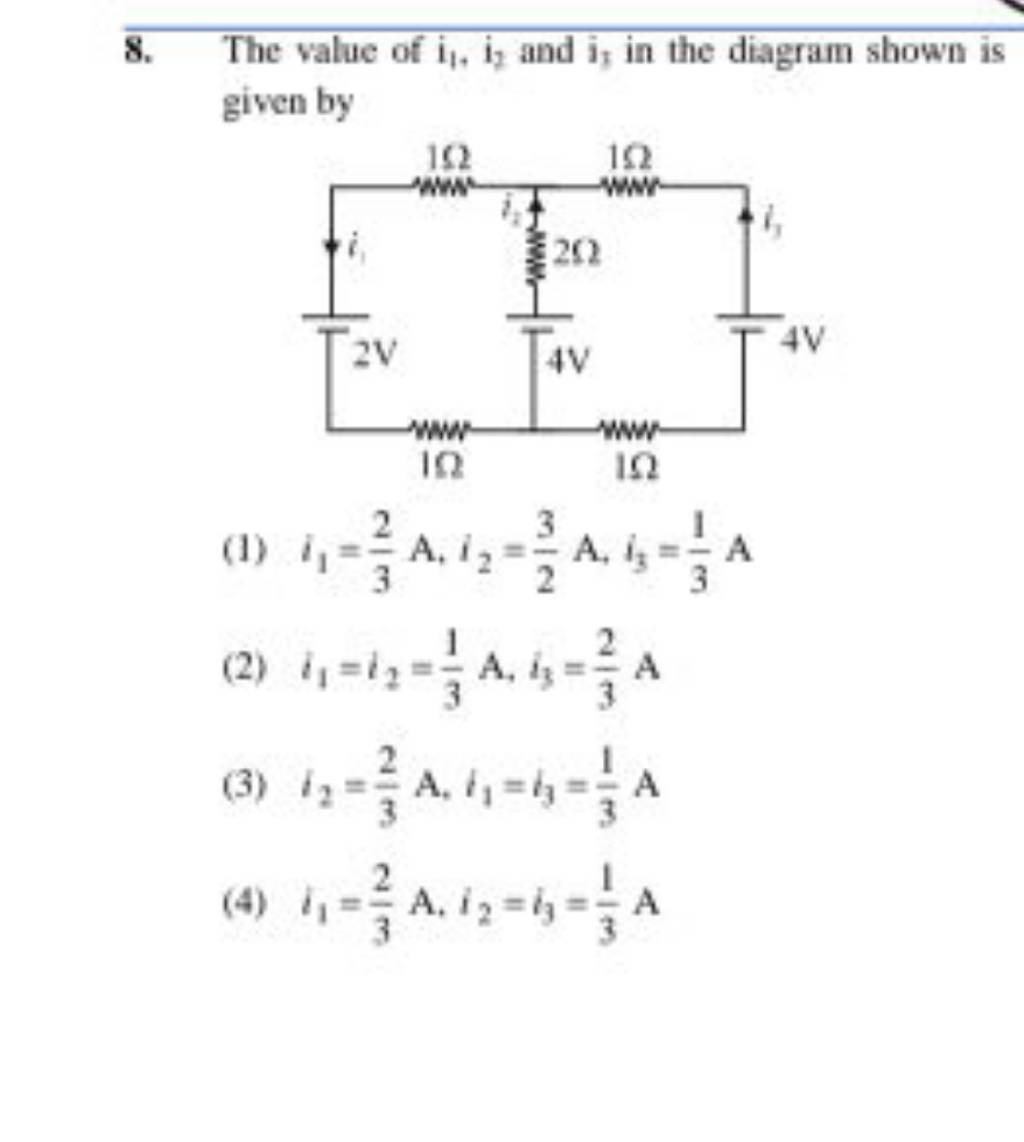
The Value Of I1 ,i2 And I3 In Diagram Shown Is Given By Filo
Real-World Applications
4. Why Knowing I3 Matters
Okay, finding I3 is cool and all, but why should you care? Well, understanding current flow is essential for designing and troubleshooting electrical circuits. Imagine you're designing a power supply for your new gadget. You need to know how much current each component is drawing to make sure you don't overload anything and cause a meltdown (literally!).
Knowing the current flowing through different parts of a circuit also helps you diagnose problems. If a component isn't getting enough current, it might not be working correctly. Or, if a component is getting too much current, it could overheat and fail. By measuring currents and comparing them to expected values, you can pinpoint the source of the problem.
Furthermore, this simple concept extends to more complex circuit analysis techniques. Once you grasp Kirchhoff's Laws, you can tackle larger and more intricate circuits, which are the building blocks of virtually all electronic devices, from your smartphone to your refrigerator.
From designing efficient circuits to troubleshooting existing ones, the ability to calculate currents like I3 is a fundamental skill for any aspiring electrician, electronics hobbyist, or engineer. So keep practicing, and you'll be a circuit-solving pro in no time!

The Value Of I1 And I2 Are Physics Questions A.4a, 3a B.3a, 4a C.4a
Troubleshooting and Common Mistakes
5. Stay Sharp, Avoid These Errors
Even with a clear understanding of KCL, it's easy to make mistakes, especially when dealing with complex circuits. One common error is forgetting to pay attention to the direction of current flow. Always double-check your assumptions and make sure you're using the correct sign convention. A simple misplaced sign can throw off your entire calculation.
Another pitfall is misidentifying the nodes in a circuit. A node is a point where two or more circuit elements are connected. Make sure you're applying KCL at the correct nodes and including all the currents entering and leaving that node.
Also, ensure you're using consistent units. Current is measured in Amperes (A), so make sure all your values are in Amperes before you start calculating. Mixing up units (like using milliamps instead of amps) can lead to wildly inaccurate results.
Finally, don't be afraid to use a circuit simulator to verify your calculations. These tools allow you to build and simulate circuits virtually, so you can check your answers and identify any errors. Practice makes perfect and simulation is a great way to ensure that you are correct.

FAQ
6. Q
A: You can assume a direction. If your calculation results in a negative current value, it just means the actual direction is opposite to what you initially assumed. The magnitude will still be correct!
7. Q
A: Yes, but you need to use complex numbers to represent the alternating currents and voltages. It gets a bit more advanced, but the fundamental principle remains the same: the sum of currents entering a node must equal the sum of currents leaving the node.
8. Q
A: Kirchhoff's Current Law still applies! Just include all the currents in your equation, making sure to pay attention to their directions (signs). The more currents, the longer the equation, but the concept is identical.